4 Aim 1 - A CLOC simulation testbed
Rationale
CLOC experiments can be difficult and costly, posing a barrier to entry for neuroscientists that find CLOC’s advantages attractive. Their lab might lack the funds or time to invest in hardware and software infrastructure or the confidence that such an investment would yield successful experiments. Moreover, when the proposed experiment requires signal processing/control method development, iterating on designs in-vivo may be cumbersome, given the additional cost of animal care and training. However, these costs and risks can be mitigated through in-silico prototyping. Given a reliable model of the system of interest, one can simulate an experiment and assess its effectiveness. Alternate models of a system can be tested to assess robustness of a method to unknown model properties, or that method can be validated on a variety of systems to determine its general applicability. This strategy not only allows for a researcher to evaluate and optimize methods before committing significant resources to them, but also accelerates the development cycle.
Innovation
For these reasons, I have developed Cleo: Closed Loop, Electrophysiology, and Optogenetics experiment simulation testbed. Unlike existing software, Cleo simultaneously provides a high-level interface to fast and flexible neural network simulations; easy, model-independent injection of electrode recording and optogenetic perturbations; and a real-time, closed-loop processing module capable of modeling communication and processing delays inherent in real experiments. I thus provide a low-cost environment to design and develop CLOC methods, as well as for researchers to see if CLOC may serve their research agenda.
Approach
Guiding principles
Two factors drove our choice of recording and stimulation models to integrate into Cleo. First, because a main purpose of Cleo is to enable prototyping of experiments, we focused on models at the level of the parameters an experimenter is able to alter—this led us to choose models embedded in physical, 3D space. Second, we assumed that highly realistic models of individual neurons are not needed to capture most mesoscale-level phenomena. Accordingly, Cleo was developed with the intention of using point neurons models, rather than multi-compartment neuron models with realistic morphologies.
In addition to our modeling priorities, the goals of usability and extensibility guided our choices in software dependencies and infrastructure. Ease of use is important to make Cleo as accessible as possible to researchers with varied backgrounds, and motivated Cleo’s modular design, which allows users to add different recording or stimulation devices with little or no modification to the underlying network model. Additionally, extensibility is important for the testbed to remain relevant under changing needs in the future, allowing for new functionality to be easily added in a “plug-in,” modular architecture.
Closed-loop simulation architecture
We chose Brian 2 (1) as the spiking neural network simulator to build Cleo around. Brian has the advantages of being flexible and intuitive, where models are defined with user-provided mathematical equations. Moreover, it is written in Python, an open-source, intuitive language (2) widely used in computational neuroscience (3, 4)—users do not need to use any other languages to use Brian and Cleo. Brian is also relatively fast (especially since it is developed primarily for point neuron simulations), as shown in benchmarks (1).
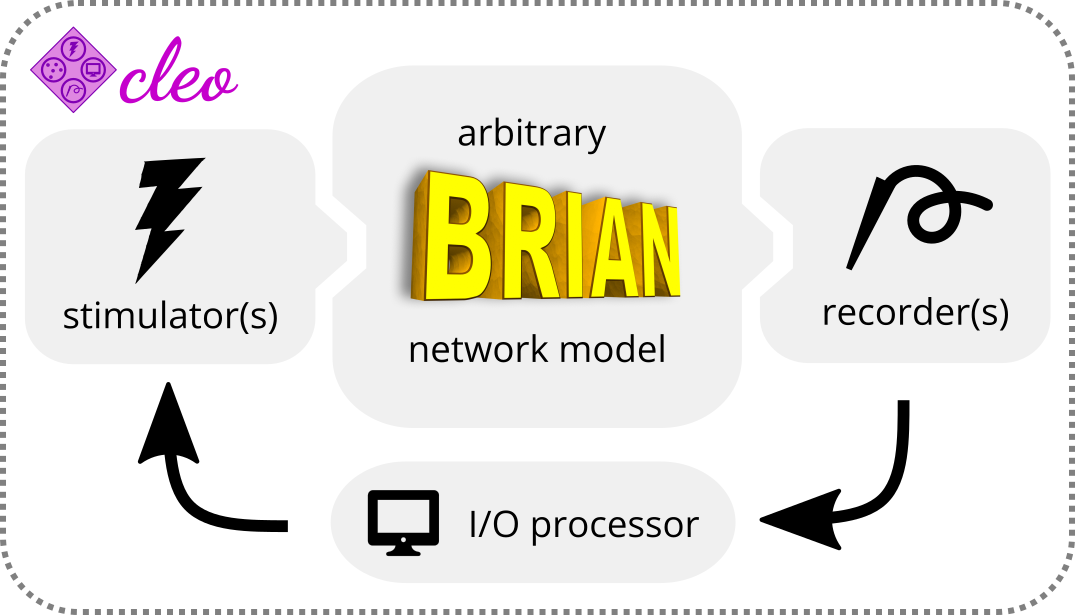
Cleo provides three modules—recording, stimulation, and closed-loop processing—for integration with an existing Brian model (see Figure 4.1). Cleo’s functionality centers around a CLSimulator object that orchestrates the interactions between these three modules and the Brian simulation by injecting devices, running the simulation, and communicating with an IOProcessor object at each time step. The IOProcessor receives recorder measurements according to a specified sampling rate and returns any updates to stimulator devices. To simulate the effects of latency in closed-loop control, Cleo provides a LatencyIOProcessor class which stores control signals in a buffer to later deliver them after an arbitrary delay.
Electrode recording
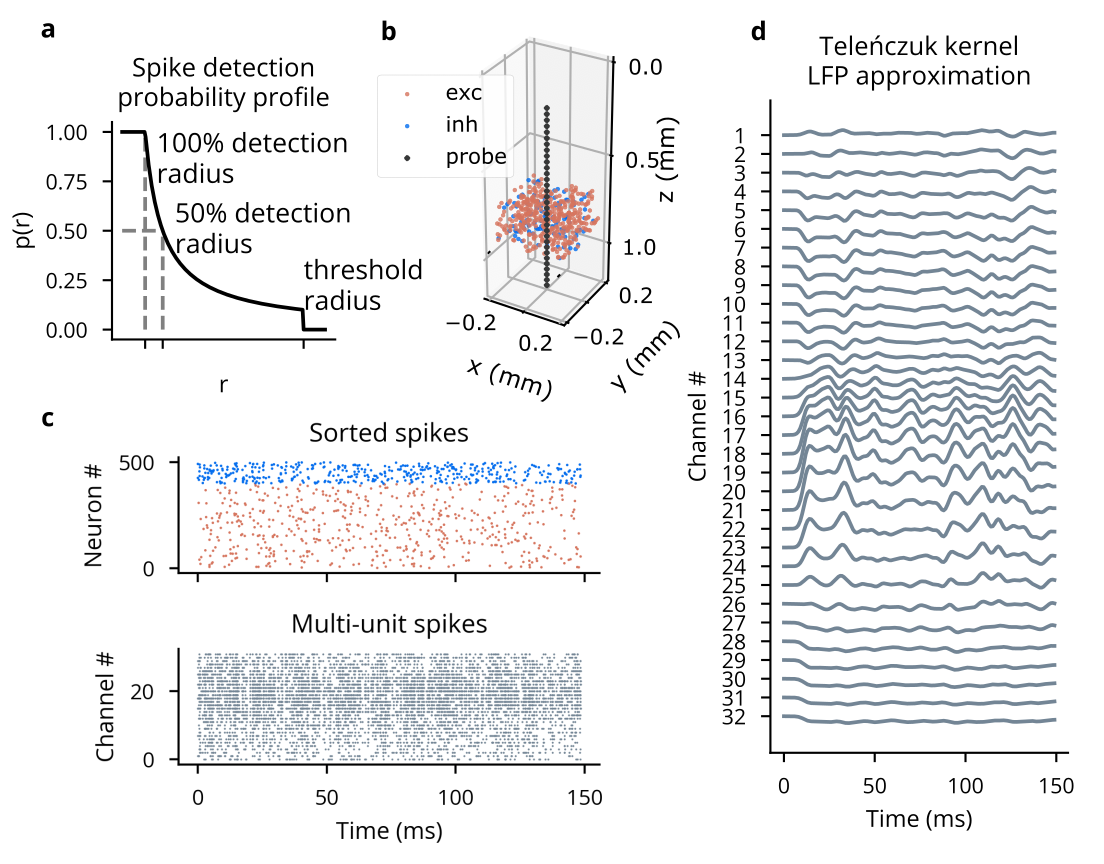
Because we have prioritized point neuron simulations, the electrode functionality currently implemented in Cleo does not rely on raw extracellular potentials, which can only be computed from multi-compartment neurons (5, 6). This biophysical forward modeling approach has been taken in other software (7–10). To approximate sorted and multi-spike recording without filtering and thresholding of extracellular potentials, Cleo simply takes ground-truth spikes and stochastically determines which to report with probability inversely proportional to distance to the electrode (11, 12) (see Figure 4.2).
In order to approximate cortical LFP without recurring to morphological neurons and biophysical forward modeling, we implemented the kernel LFP approximation from (13), which we term TKLFP (Teleńczuk kernel LFP). This method approximates the per-spike contribution to LFP (termed uLFP: unitary LFP) with a delayed Gaussian function, where amplitude and delay depend on the position of the neuron relative to the electrode. This implementation is available as a standalone Python package on PyPI (14). Accuracy of this implementation is verified in automated test suites in both TKLFP and Cleo packages.
Optogenetic stimulation
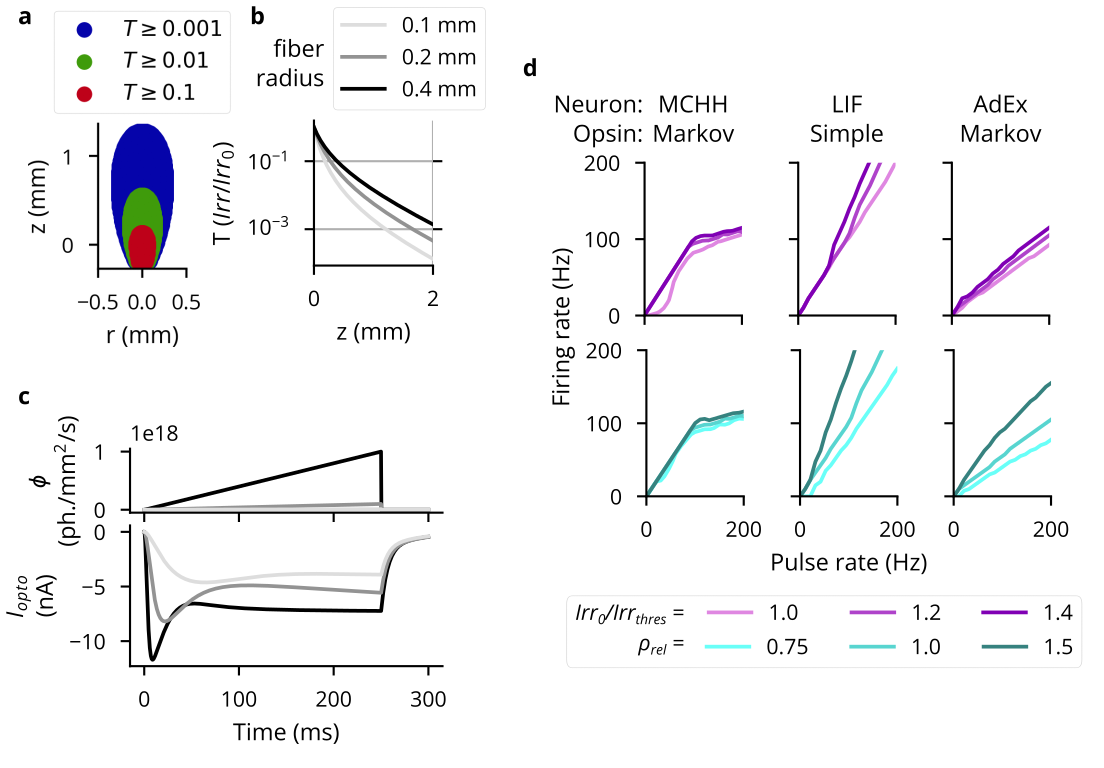
Cleo simulates optogenetic stimulation by combining a model of light propagation with an opsin model relating light to current. The light model is based on Kubelka-Munk light propagation, operating on the assumption that the medium is optically homogeneous and that particles are larger than the light wavelength (15, 16). Cleo includes absorbance, scattering, and refraction parameters for 473-nm (blue) light as given in (15).
Independent of the light propagation model, Cleo provides two different opsin models. One is a four-state Markov model as presented in (17), which captures rise, peak, plateau, and fall dynamics as the opsin is activated and deactivated through a Markov process. Additionally, by defining conductance rather than current directly, the model is able to reproduce the photocurrent’s dependence on the membrane potential (see Figure 4.3). Because the Markov model depends on somewhat realistic membrane potential and resistance values, however, it is not well suited for many pre-existing models that do not. To that end, Cleo also provides a simplified model that delivers current (of arbitrary units) proportional to light at the neuron. Users can also specify both the probability that cells of a target population express an opsin and the per-cell expression level.
Results
Model validation
To verify that light and opsin models behaved as expected, we reproduced figures illustrating the optic fiber light transmission profile found in Figure 2a,b of (15) and the photocurrent in response to the ramping light intensity from Figure 4c of (17). Light intensity-firing rate relationship was qualitatively similar to that originally reported, though differing in some respects due to the use of point neurons rather than morphological neurons. See Figure 4.3 for details. Additionally, preliminary experiments show that the simplified, proportional current opsin model is able to produce a firing response qualitatively similar to that of the Markov model.
Example experiments
In order to demonstrate Cleo’s utility to the public, we implemented three example experiments to feature in the upcoming publication:
- Closed-loop inhibition of a traveling wave in a rodent somatosensory cortex model (19). This experiment features a simple on/off control scheme where light activating an inhibitory opsin is turned on whenever the number of spikes detected at the optrode exceeds a threshold. The result is that while a wave of activity spreads outward through sensory cortex in response to a stimulus, the area around the optrode remains unperturbed. An experiment of this sort could explore the consequences of traveling waves in sensory cortex on perception.
- Feedback control of layer 2/3 interneurons, disrupting plasticity in a model of primary visual cortex (20). In this model, a top-down reward signal to vasoactive intestinal peptide (VIP) interneurons inhibits a population of parvalbumin (PV) interneurons, in turn disinhibiting a population of pyramidal cells (PC). However, using a proportional-integral (PI) feedback controller, we clamp the firing rate of interneurons, blocking this disinhibtion. Without increased PC firing, synaptic weights corresponding to the rewarded stimulus no longer increase, thus demonstrating how feedback control can disrupt normal circuit function.
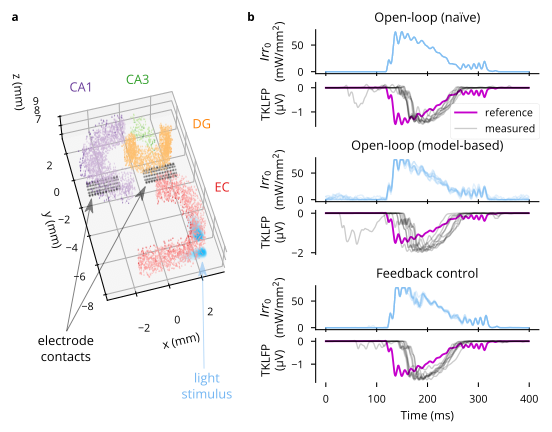
- Optogenetic evocation of sharp wave-ripples in an anatomically detailed model of hippocampus (21, 22). This uses linear quadratic regulator control to evoke a reference sharp wave-ripple LFP signature. See Figure 4.4 for details, and note that feedback control, not looking ahead, so to speak, fails to evoke the reference signal at the desired time. The strategy I propose in Aim 2 should remedy this.
Additionally, we have endeavored to make Cleo accessible to the public to aid in the exploration and adoption of CLOC methods. Cleo is open-source and can be installed from the Python Package Index under the name cleosim. The code can be found on GitHub. Documentation, including an overview, tutorials, and API reference, can be found at https://cleosim.readthedocs.io.
Limitations
Because we (and Brian) prioritize point neuron models, Cleo does not currently support advanced, morphology-dependent features of neural dynamics as well as recording and stimulation. This would preclude realistically simulating extracellular potentials as well as the effects of spike sorting, for example. However, if features such as these are needed, Cleo could be developed further to integrate with Brian’s morphological neuron features. And in the case of LFP, at least one other method exists for point-neuron LFP approximation which could be implemented to help compensate for the limitations of TKLFP (23).
Both a strength and a limitation of Cleo’s design is that it depends on whatever model the user provides. This avoids the pitfall of painstakingly developing stock models that may or may not prove useful to researchers and instead lets them identify or develop a model that adequately describes the phenomena being studied. If a sufficiently realistic model for the studied system does not exist, however, developing one may be prohibitively costly, becoming a computational project in its own right as opposed to simply a stepping-stone towards an experiment. In these cases we suggest that a workaround could be to test a variety of potential models to identify which experimental configurations would be robust to unknown properties of the system. Indeed, the desired experiment in this case could be one that best adjudicates between these hypotheses.
Summary of contributions
Cleo thus provides a simulation environment facilitating and accelerating the adoption and development of CLOC methods. Multiple features were designed to reflect this need, for example, neural simulation and experimental configuration at an intermediate level of realism, relevant recording and stimulation modalities, modular software architecture, flexible interfacing that can be easily adapted to existing Brian models, and arbitrary closed-loop processing enabling realistic processing delays. Moreover, we have developed virtual experiments to serve as examples as well as thorough online documentation so Cleo can help experimental labs test and potentially adopt CLOC methods.